Булевы функции и формулы
В этом разделе вы найдете бесплатные примеры решений базовых задач по булевым формулам (формулам булевой алгебры): упрощение формул, проверка на тавтологию, преобразование к виду без скобок, проверка фиктивности переменной, доказательство эквивалентности булевых формул и т.п.
В следующих разделах вы найдете другие примеры решений о булевых функциях:
Есть трудности с задачами? МатБюро поможет вам: дискретная математика на заказсдача дистанционных тестов.
Решения задач по булевым формулам онлайн
Задача 1. Проверить, является ли тавтологией формула: $a \& b \to(a \& b \vee c \vee \bar c)$
Задача 2. Преобразовать данную формулу так, чтобы она содержала только операции тесного отрицания, дизъюнкции и конъюнкции. Пользуясь свойствами операций дизъюнкции и конъюнкции, привести формулу к виду, не содержащему скобок.
$$(\overline {x_1} \vee x_2) \to (\overline {x_1}\sim x_3)\overline {x_3} $$Задача 3. Показать, что $x_1$ - фиктивная переменная функции $f$ (реализовав для этой цели функцию $f$ формулой, не содержащей явно переменную $x_1$).
Задача 4. Используя приведенные ниже (основные) эквивалентности и соотношения, доказать эквивалентность формул $U$ и $B$.
Задача 5. Классифицировать формулу $\overline{ (\overline{xy}\to x) \vee y}$
Булева алгебра для чайников
Булева алгебра
Булевой алгеброй называется непустое множество $A$ с двумя бинарными операциями $\land$ (аналог конъюнкции), $\lor $ (аналог дизъюнкции), одной унарной операцией $\lnot$ (аналог отрицания) и двумя выделенными элементами: 0 (или Ложь) и 1 (или Истина) такими, что для любых a, b и c из множества A верны следующие аксиомы:
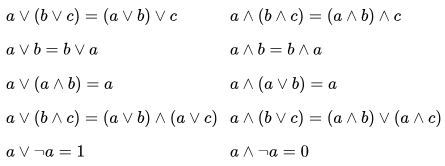
Логические операции
В алгебре логики основными (элементарными) операциями являются отрицание, логическое сложение (дизъюнкция), логическое умножение (конъюнкция), импликация, эквивалентность.
Основные формулы по алгебре логики: функции алгебры логики, таблица истинности, основные эквивалентности, преобразование к конъюнкции, дизъюнкции и отрицанию
Приоритет логических операций
При упрощении булевых формул или высказываний, связанных скобками и логическими операциями, используют следующие правила приоритета (или старшинства) логических операций - от наиболее сильной - к слабой:
$$ \neg \quad \wedge \quad \vee \quad \to \quad \leftrightarrow $$Словесно: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.




